www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Matriks ›
Diketahui matriks \( P = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \) dan \( Q = \begin{bmatrix} 5 & 4 \\ 1 & 1 \end{bmatrix} \). Jika \( P^{-1} \) adalah invers matriks P dan \( Q^{-1} \) adalah invers matriks Q, maka determinan dari \( P^{-1} Q^{-1} \) adalah…
- 223
- 1
- -1
- -10
- -223
(UN 2008)
Pembahasan:
Pertama, kita cari determinan dari matriks P dan Q terlebih dahulu, yakni:

Selanjutnya, berdasarkan sifat determinan, \( |PQ| = |P||Q| \) dan \( |A^{-1}| = \frac{1}{|A|} \). Dengan demikian, determinan dari \( P^{-1} Q^{-1} \), yaitu:
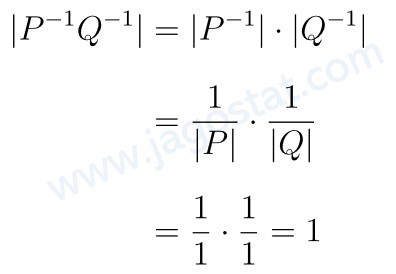
Jawaban B.